Esmalt tutvustame eksponentsiaalfunktsiooni definitsiooni.
Eksponentfunktsioon $f\left(x\right)=a^x$, kus $a >1$.
Tutvustame eksponentsiaalfunktsiooni omadusi $a >1$ korral.
\ \ [juuri pole\] \
Ristumine koordinaattelgedega. Funktsioon ei lõiku $Ox$ teljega, vaid lõikub $Oy$ teljega punktis $(0,1)$.
$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$
\ \ [juuri pole\] \
Graafik (joonis 1).
Joonis 1. Funktsiooni $f\left(x\right)=a^x,\ graafik \ a >1$ jaoks.
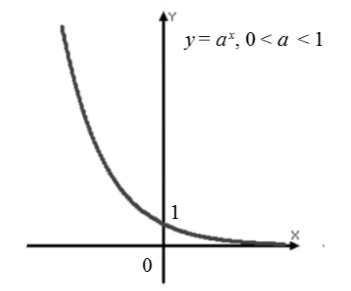
Eksponentfunktsioon $f\left(x\right)=a^x$, kus $0
Tutvustame eksponentsiaalfunktsiooni omadusi $0 jaoks
Määratluspiirkond on kõik reaalarvud.
$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- funktsioon pole paaris ega paaritu.
$f(x)$ on pidev kogu määratluspiirkonnas.
Väärtuste vahemik on intervall $(0,+\infty)$.
$f"(x)=\left(a^x\right)"=a^xlna$
\ \ [juuri pole\] \ \ [juuri pole\] \
Funktsioon on kumer kogu määratluspiirkonnas.
Käitumine ulatuse lõpus:
\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]
Graafik (joonis 2).
Näide ülesandest eksponentsiaalfunktsiooni konstrueerimiseks
Uurige ja joonistage funktsioon $y=2^x+3$.
Lahendus.
Teeme uuringu ülaltoodud skeemi näitel:
Määratluspiirkond on kõik reaalarvud.
$f\left(-x\right)=2^(-x)+3$ -- funktsioon pole paaris ega paaritu.
$f(x)$ on pidev kogu määratluspiirkonnas.
Väärtuste vahemik on intervall $(3,+\infty)$.
$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$
Funktsioon suureneb kogu määratluspiirkonna ulatuses.
$f(x)\ge 0$ kogu määratluspiirkonna ulatuses.
Ristumine koordinaattelgedega. Funktsioon ei lõiku $Ox$ teljega, vaid lõikub $Oy$ teljega punktis ($0,4)$
$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$
Funktsioon on kumer kogu määratluspiirkonnas.
Käitumine ulatuse lõpus:
\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\]
Graafik (joonis 3).

Joonis 3. Funktsiooni $f\left(x\right)=2^x+3$ graafik
Eksponentfunktsioon
Funktsioon kujul y = a x , kus a on suurem kui null ja a ei ole võrdne ühega, nimetatakse eksponentsiaalfunktsiooniks. Eksponentfunktsiooni peamised omadused:
1. Eksponentfunktsiooni domeeniks on reaalarvude hulk.
2. Eksponentfunktsiooni vahemik on kõigi positiivsete reaalarvude hulk. Mõnikord on seda komplekti lühiduse huvides tähistatud kui R+.
3. Kui eksponentsiaalfunktsioonis on alus a suurem kui üks, siis funktsioon kasvab kogu definitsioonipiirkonna ulatuses. Kui aluse a eksponentsiaalfunktsioon vastab järgmisele tingimusele 0
4. Kehtivad kõik kraadide põhiomadused. Kraadide põhiomadusi esindavad järgmised võrdsused:
a x *a y = a (x+y) ;
(a x )/(a y ) = a (x-y) ;
(a*b) x = (a x )*(a y );
(a/b) x = a x /b x ;
(a x ) y = a (x*y) .
Need võrdsused kehtivad kõigi x ja y reaalväärtuste puhul.
5. Eksponentfunktsiooni graafik läbib alati punkti koordinaatidega (0;1)
6. Sõltuvalt sellest, kas eksponentsiaalfunktsioon suureneb või väheneb, on selle graafikul üks kahest tüübist.
Järgmisel joonisel on kujutatud kasvava eksponentsiaalfunktsiooni graafik: a>0.
Järgmine joonis on kahaneva eksponentsiaalfunktsiooni graafik: 0

Punkti (0; 1) läbivad nii kasvava eksponentsiaalfunktsiooni kui ka kahaneva eksponentsiaalfunktsiooni graafik vastavalt viiendas lõigus kirjeldatud omadusele.
7. Eksponentfunktsioonil ei ole äärmuspunkte, ehk teisisõnu tal puuduvad funktsiooni miinimum- ja maksimumpunktid. Kui arvestame funktsiooni mis tahes konkreetsel segmendil, võtab funktsioon selle intervalli lõpus minimaalsed ja maksimaalsed väärtused.
8. Funktsioon ei ole paaris ega paaritu. Eksponentfunktsioon on üldfunktsioon. Seda on näha ka graafikutelt, ükski neist pole sümmeetriline ei Oy telje ega ka alguspunkti suhtes.
Logaritm

Logaritme on koolimatemaatika kursuses alati raskeks teemaks peetud. Logaritmi definitsioone on palju erinevaid, kuid millegipärast kasutatakse enamikes õpikutes neist kõige keerulisemat ja kahetsusväärsemat.
Logaritmi määratleme lihtsalt ja selgelt. Koostame selle jaoks tabeli:
Niisiis, meil on kaks jõudu. Kui võtate numbri alumiselt realt, saate hõlpsalt leida võimsuse, milleni peate selle numbri saamiseks kahe tõstma. Näiteks 16 saamiseks peate kahe tõstma neljanda astmeni. Ja 64 saamiseks peate tõstma kaks kuuenda astmeni. Seda on tabelist näha.
Ja nüüd - tegelikult logaritmi määratlus:
Definitsioon
Logaritm alus a argumendist x on võimsus, milleni numbrit tuleb tõsta a numbri saamiseks x.
Määramine
log a x = b
kus a on alus, x on argument, b Mis täpselt on logaritm.
Näiteks 2 3 = 8 ⇒ log 2 8 = 3 (aluse 2 logaritm 8-st on kolm, sest 2 3 = 8). Sama hästi võiks logida 2 64 = 6, sest 2 6 = 64.
Nimetatakse arvu antud baasi logaritmi leidmise operatsioonilogaritm . Nii et lisame oma tabelisse uue rea:
Kahjuks kõiki logaritme nii lihtsalt ei käsitleta. Näiteks proovige leida log 2 5. Arv 5 ei ole tabelis, kuid loogika näeb ette, et logaritm asub kuskil lõigul. Sest 22< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Selliseid numbreid nimetatakse irratsionaalseteks: koma järel olevaid numbreid saab kirjutada lõputult ja need ei kordu kunagi. Kui logaritm osutub irratsionaalseks, on parem jätta see nii: log 2 5, log 3 8, log 5 100.
Oluline on mõista, et logaritm on kahe muutujaga avaldis (alus ja argument). Alguses ajavad paljud segadusse, kus on alus ja kus on argument. Ärritavate arusaamatuste vältimiseks vaadake lihtsalt pilti:
Meie ees pole midagi muud kui logaritmi määratlus. Pidage meeles: logaritm on võimsus , millele argumendi saamiseks peate aluse tõstma. See on alus, mis tõstetakse võimsusele - pildil on see punasega esile tõstetud. Selgub, et alus on alati põhjas! Räägin seda imelist reeglit oma õpilastele juba esimeses tunnis – ja seal pole segadust.
Mõistsime definitsiooni välja – jääb üle õppida logaritme lugema, s.t. "logi" märgist lahti saada. Alustuseks märgime, et Määratlusest tuleneb kaks olulist fakti:
Argument ja alus peavad alati olema suuremad kui null. See tuleneb astme määratlusest ratsionaalse astendajaga, millele logaritmi definitsioon taandatakse.
Alus peab erinema ühtsusest, kuna ühik mis tahes võimsusele on ikkagi üksus. Seetõttu on mõttetu küsimus “millisele võimule tuleb tõsta, et saada kaks”. Sellist kraadi pole olemas!
Sellised piirangud helistas kehtiv vahemik(ODZ). Selgub, et logaritmi ODZ näeb välja selline: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Märka seda arvul pole piirangut b (logaritmi väärtus) ei kattu. Näiteks võib logaritm olla negatiivne: log 2 0,5 = −1, sest 0,5 = 2-1.
Kuid nüüd käsitleme ainult arvulisi avaldisi, kus pole vaja teada logaritmi ODZ-d. Kõiki piiranguid on probleemide koostajad juba arvesse võtnud. Kui aga mängu tulevad logaritmilised võrrandid ja ebavõrdsused, muutuvad DHS-i nõuded kohustuslikuks. Tõepoolest, aluses ja argumendis võivad olla väga tugevad konstruktsioonid, mis ei pruugi ülaltoodud piirangutele vastata.
Nüüd arvestage kindraliga logaritmide arvutamise skeem. See koosneb kolmest etapist:
Esitage sihtasutus a ja argument x astmena, mille väikseim võimalik alus on suurem kui üks. Teel on parem kümnendmurdudest lahti saada;
Otsustage muutuja kasuks b võrrand: x = a b ;
Saadud number b on vastus.
See on kõik! Kui logaritm osutub irratsionaalseks, on seda näha juba esimesel sammul. Nõue, et baas peab olema suurem kui üks, on väga asjakohane: see vähendab vea tõenäosust ja lihtsustab oluliselt arvutusi. Samamoodi kümnendmurdudega: kui need kohe tavalisteks teisendada, siis on vigu kordades vähem.
Vaatame konkreetsete näidete abil, kuidas see skeem töötab:
Arvutage logaritm: log 5 25
Esitame alust ja argumenti viie astmena: 5 = 5 1 ; 25 = 52;
Koostame ja lahendame võrrandi:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
Sai vastuse: 2.
Arvutage logaritm:
Esitame alust ja argumenti kolme astmena: 3 = 3 1 ; 1/81 \u003d 81 -1 \u003d (3 4) -1 \u003d 3 -4;
Koostame ja lahendame võrrandi:
Sain vastuse: -4.
−4
Arvutage logaritm: log 4 64
Esitame alust ja argumenti kahe astmena: 4 = 2 2 ; 64 = 26;
Koostame ja lahendame võrrandi:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
Sai vastuse: 3.
Arvutage logaritm: log 16 1
Esitame alust ja argumenti kahe astmena: 16 = 2 4 ; 1 = 20;
Koostame ja lahendame võrrandi:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
Sai vastuse: 0.
Arvutage logaritm: log 7 14
Esitame alust ja argumenti seitsme astmena: 7 = 7 1 ; 14 ei ole esitatud seitsme astmena, sest 7 1< 14 < 7 2 ;
Eelmisest lõigust järeldub, et logaritmi ei arvestata;
Vastus ei muutu: logi 7 14.
logi 7 14
Väike märkus viimase näite kohta. Kuidas teha kindlaks, et arv ei oleks teise arvu täpne aste? Väga lihtne – lihtsalt jagage see algteguriteks. Kui laienemisel on vähemalt kaks erinevat tegurit, ei ole see arv täpne võimsus.
Uurige, kas arvu täpsed astmed on: 8; 48; 81; 35; neliteist.
8 \u003d 2 2 2 \u003d 2 3 - täpne kraad, sest on ainult üks kordaja;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 ei ole täpne võimsus, sest tegureid on kaks: 3 ja 2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - täpne kraad;
35 = 7 5 - jällegi mitte täpne kraad;
14 \u003d 7 2 - jällegi mitte täpne kraad;
8, 81 - täpne kraad; 48, 35, 14 - ei.
Pange tähele ka seda, et algarvud ise on alati iseenda täpsed astmed.
Kümnendlogaritm
Mõned logaritmid on nii levinud, et neil on eriline nimi ja tähistus.
Definitsioon
Kümnendlogaritm argumendist x on logaritm alusele 10, st. võimsus, milleni peate numbri saamiseks tõstma arvu 10 x.
Määramine
lg x
Näiteks log 10 = 1; log 100 = 2; lg 1000 = 3 - jne.
Nüüdsest, kui õpikusse ilmub fraas nagu “Leia lg 0,01”, teadke, et see pole kirjaviga. See on kümnendlogaritm. Kui te pole aga sellise nimetusega harjunud, saate selle alati ümber kirjutada:
log x = log 10 x
Kõik, mis kehtib tavaliste logaritmide puhul, kehtib ka kümnendkohtade puhul.
naturaallogaritm
On veel üks logaritm, millel on oma tähistus. Mõnes mõttes on see isegi olulisem kui kümnend. See on loomulik logaritm.
Definitsioon
naturaallogaritm argumendist x on baaslogaritm e , st. võimsus, milleni tuleb numbrit tõsta e numbri saamiseks x.
Määramine
ln x
Paljud küsivad: mis on number e? See on irratsionaalne arv, selle täpset väärtust pole võimalik leida ja üles kirjutada. Siin on vaid esimesed numbrid:
e = 2,718281828459...
Me ei hakka süvenema sellesse, mis see number on ja milleks seda vaja on. Pidage vaid meeles, et e on naturaallogaritmi alus:
ln x = log e x
Seega ln e = 1; log e 2 = 2; Kell 16 = 16 - jne. Teisest küljest on ln 2 irratsionaalne arv. Üldiselt on mis tahes ratsionaalarvu naturaallogaritm irratsionaalne. Välja arvatud muidugi ühtsus: ln 1 = 0.
Naturaallogaritmide puhul kehtivad kõik reeglid, mis kehtivad tavaliste logaritmide puhul.
Logaritmide põhiomadused
Logaritme, nagu iga arvu, saab igal võimalikul viisil liita, lahutada ja teisendada. Kuid kuna logaritmid pole päris tavalised arvud, on siin reeglid, mida nimetatakse põhiomadusteks.
Neid reegleid tuleb teada – ilma nendeta ei saa lahendada ühtegi tõsist logaritmilist ülesannet. Lisaks on neid väga vähe – ühe päevaga saab kõik selgeks. Nii et alustame.
Logaritmide liitmine ja lahutamine
Vaatleme kahte sama alusega logaritmi: log a x ja logi a y . Seejärel saab neid liita ja lahutada ning:
logi a x +logi jah = log a ( x · y );
logi a x −logi jah = log a ( x : y ).
Niisiis, logaritmide summa võrdub korrutise logaritmiga ja erinevus on jagatise logaritm. Pange tähele: võtmepunkt on siin samad alused. Kui alused on erinevad, siis need reeglid ei tööta!
Need valemid aitavad teil arvutada logaritmilise avaldise isegi siis, kui selle üksikuid osi ei arvestata (vt õppetundi " "). Vaadake näiteid ja vaadake:
Leidke avaldise väärtus: log 6 4 + log 6 9.
Kuna logaritmide alused on samad, kasutame summa valemit:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Leidke avaldise väärtus: log 2 48 − log 2 3.
Alused on samad, kasutame erinevuse valemit:
log 2 48 – log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Leidke avaldise väärtus: log 3 135 − log 3 5.
Jällegi on alused samad, seega on meil:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Nagu näete, koosnevad algsed avaldised "halbadest" logaritmidest, mida eraldi ei käsitleta. Kuid pärast teisendusi ilmnevad üsna tavalised numbrid. Paljud testid põhinevad sellel faktil. Jah, seda kontrolli – sarnaseid väljendeid täie tõsidusega (mõnikord – praktiliselt ilma muudatusteta) pakutakse eksamil.
Astendaja eemaldamine logaritmist
Teeme nüüd ülesande pisut keerulisemaks. Mis siis, kui logaritmi baasis või argumendis on aste? Siis selle astme eksponendi saab logaritmi märgist välja võtta järgmiste reeglite järgi:
On lihtne mõista, et viimane reegel järgib nende kahte esimest. Kuid parem on see ikkagi meeles pidada - mõnel juhul vähendab see arvutuste mahtu märkimisväärselt.
Muidugi kõik need reeglid on mõistlikud, kui järgitakse ODZ logaritmi: a > 0, a ≠ 1, x > 0 logaritmi endasse saab sisestada arvud enne logaritmi märki. See on see, mida kõige sagedamini nõutakse.
Leidke avaldise väärtus: log 7 49 6 .
Vabaneme argumendi astmest esimese valemi järgi:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Leidke avaldise väärtus:
Pange tähele, et nimetaja on logaritm, mille alus ja argument on täpsed astmed: 16 = 2 4 ; 49 = 72. Meil on:

Ma arvan, et viimane näide vajab selgitust. Kuhu kadusid logaritmid? Kuni viimase hetkeni töötame ainult nimetajaga. Nad esitasid seal seisva logaritmi aluse ja argumendi kraadidena ning võtsid välja indikaatorid - nad said “kolmekorruselise” murru.
Vaatame nüüd põhifraktsiooni. Lugejal ja nimetajal on sama arv: log 2 7. Kuna log 2 7 ≠ 0, saame murdosa vähendada - 2/4 jääb nimetajasse. Aritmeetika reeglite järgi saab nelja üle kanda lugejasse, mis ka tehti. Tulemuseks on vastus: 2.
Üleminek uuele vundamendile
Rääkides logaritmide liitmise ja lahutamise reeglitest, rõhutasin konkreetselt, et need töötavad ainult samade alustega. Mis siis, kui alused on erinevad? Mis siis, kui need ei ole sama arvu täpsed astmed?
Appi tulevad valemid uuele baasile üleminekuks. Sõnastame need teoreemi kujul:
Teoreem
Laske logaritmil logida a x . Siis suvalise numbri jaoks c nii, et c > 0 ja c ≠ 1, võrdsus on tõene:
![]()
Eelkõige, kui paneme c = x, saame:
![]()
Teisest valemist järeldub, et logaritmi alust ja argumenti on võimalik omavahel vahetada, kuid sel juhul “pööratakse ümber” kogu avaldis, s.t. logaritm on nimetajas.
Neid valemeid leidub tavalistes arvavaldistes harva. Seda, kui mugavad need on, saab hinnata ainult logaritmiliste võrrandite ja võrratuste lahendamisel.
Siiski on ülesandeid, mida ei saa üldse lahendada, välja arvatud uuele sihtasutusele kolimine. Vaatleme paari neist:
Leidke avaldise väärtus: log 5 16 log 2 25.
Pange tähele, et mõlema logaritmi argumendid on täpsed eksponendid. Võtame välja näitajad: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;
Nüüd pöörame teise logaritmi ümber:
Kuna korrutis tegurite permutatsioonist ei muutu, korrutasime rahulikult nelja ja kahega ning siis mõtlesime välja logaritmid.
Leidke avaldise väärtus: log 9 100 lg 3.
Esimese logaritmi alus ja argument on täpsed võimsused. Paneme selle kirja ja vabaneme näitajatest:
Nüüd vabaneme kümnendlogaritmist, liikudes uuele alusele:
Põhiline logaritmiline identiteet
Sageli on lahendamise käigus vaja esitada arv antud baasi logaritmina. Sel juhul aitavad meid valemid:
Esimesel juhul number n muutub argumendi eksponendiks. Number n võib olla absoluutselt ükskõik, sest see on lihtsalt logaritmi väärtus.
Teine valem on tegelikult parafraseeritud määratlus. Seda nimetatakse nii:põhilogaritmiline identiteet.
Tõepoolest, mis juhtub, kui arvu b tõstetakse sellisel määral, et selle astme arv b annab arvu a? Täpselt nii: see on sama number a. Lugege see lõik uuesti hoolikalt läbi – paljud inimesed "ripuvad" selle küljes.
Nagu uued baasteisendusvalemid, on ka põhilogaritmiline identiteet mõnikord ainus võimalik lahendus.
Ülesanne
Leidke avaldise väärtus:
Lahendus
Pange tähele, et log 25 64 = log 5 8 - lihtsalt võttis ruudu baasist välja ja logaritmi argumendi. Arvestades sama baasiga võimsuste korrutamise reegleid, saame:
200
Kui keegi pole kursis, siis eksamilt oli see päris ülesanne :)
Logaritmiline ühik ja logaritmiline null
Kokkuvõtteks annan kaks identiteeti, mida on raske omadusteks nimetada – pigem on need logaritmi definitsioonist tulenevad tagajärjed. Neid leitakse pidevalt probleemidest ja üllataval kombel tekitavad nad probleeme isegi "edasijõudnud" õpilastele.
log a a = 1 on logaritmiline ühik. Pidage üks kord meeles: logaritm mis tahes baasile a sellest alusest ise on võrdne ühega.
log a 1 = 0 on logaritmiline null. Alus a võib olla ükskõik, aga kui argument on üks - logaritm on null! sest a 0 = 1 on definitsiooni otsene tagajärg.
See on kõik omadused. Harjutage kindlasti nende rakendamist!
Teadmiste hüpermarket >>Matemaatika >>Matemaatika 10. klass >>
Eksponentfunktsioon, selle omadused ja graafik
Mõelge avaldisele 2x ja leidke selle väärtused muutuja x erinevate ratsionaalsete väärtuste jaoks, näiteks kui x=2;
Üldiselt olenemata sellest, millise ratsionaalse väärtuse me muutujale x anname, saame alati arvutada avaldise 2x vastava arvväärtuse. Seega võib rääkida eksponentsiaalist funktsioonid y=2 x defineeritud ratsionaalarvude hulgal Q:
Vaatleme selle funktsiooni mõningaid omadusi.
Vara 1. on kasvav funktsioon. Tõestust teostame kahes etapis.
Esimene aste. Tõestame, et kui r on positiivne ratsionaalarv, siis 2 r >1.
Võimalikud on kaks juhtumit: 1) r on naturaalarv, r = n; 2) tavaline taandamatu murdosa,

Viimase võrratuse vasakul küljel on meil , ja paremal pool 1. Seega saab viimase võrratuse ümber kirjutada järgmiselt
Seega igal juhul kehtib ebavõrdsus 2 r > 1, nagu nõutud.
Teine faas. Olgu x 1 ja x 2 arvud ning x 1 ja x 2< х2. Составим разность 2 х2 -2 х1 и выполним некоторые ее преобразования:
(vahet x 2 -x 1 tähistasime tähega r).
Kuna r on positiivne ratsionaalarv, siis esimeses etapis tõestatuga on 2 r > 1, st. 2 r -1 >0. Arv 2x" on samuti positiivne, mis tähendab, et korrutis 2 x-1 (2 Г -1) on samuti positiivne. Seega oleme tõestanud, et ebavõrdsus 2 Xr -2x "\u003e 0.
Niisiis, võrratusest x 1< х 2 следует, что 2х" <2 x2 , а это и означает, что функция у -2х - возрастающая.
Vara 2. altpoolt piiratud ja ülalt mitte piiratud.
Funktsiooni piiritus altpoolt tuleneb võrratusest 2 x > 0, mis kehtib funktsiooni domeenist mis tahes x väärtuste korral. Samas, olenemata sellest, milline positiivne arv M võetakse, saab alati valida sellise näitaja x, et täituks võrratus 2 x > M - mis iseloomustab funktsiooni piiramatust ülalt. Toome mõned näited.

Vara 3. ei oma miinimum- ega maksimumväärtust.
See, et see funktsioon ei ole kõige olulisem, on ilmne, sest nagu me just nägime, ei ole see ülalt piiratud. Kuid see on altpoolt piiratud, miks pole sellel kõige väiksem väärtus?
Oletame, et 2r on funktsiooni väikseim väärtus (r on mingi ratsionaalne astendaja). Võtke ratsionaalne arv q<г. Тогда в силу возрастания функции у=2 х будем иметь 2 x <2г. А это значит, что 2 r не может служить наименьшим значением функции.
See kõik on hea, ütlete, aga miks me käsitleme funktsiooni y-2 x ainult ratsionaalarvude hulgal, miks me ei käsitle seda, nagu teisi tuntud funktsioone, tervel arvureal või mõnel pideval intervallil numbririda? Mis meid takistab? Mõelgem olukorrale.
Arvurida ei sisalda mitte ainult ratsionaalseid, vaid ka irratsionaalseid arve. Varem uuritud funktsioonide puhul see meid ei häirinud. Näiteks leidsime funktsiooni y \u003d x 2 väärtused võrdselt hõlpsalt nii x ratsionaalse kui ka irratsionaalse väärtuse jaoks: piisas antud x väärtuse ruudustamiseks.
Kuid funktsiooniga y \u003d 2 x on olukord keerulisem. Kui argumendile x on antud ratsionaalne väärtus, siis põhimõtteliselt saab x arvutada (naaske lõigu algusesse, kus me just seda tegime). Ja kui argumendile x antakse irratsionaalne väärtus? Kuidas näiteks arvutada? Me ei tea seda veel.
Matemaatikud on leidnud väljapääsu; nii nad rääkisid.
On teada, et ![]() Mõelge ratsionaalarvude jadale - arvu kümnendarvude lähendused puudujäägi järgi:
Mõelge ratsionaalarvude jadale - arvu kümnendarvude lähendused puudujäägi järgi:
1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... .
On selge, et 1,732 = 1,7320 ja 1,732050 = 1,73205. Selliste korduste vältimiseks jätame kõrvale need jada liikmed, mis lõpevad numbriga 0.
Siis saame kasvava järjestuse:
1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... .
Vastavalt suureneb ka järjestus.
Kõik selle jada liikmed on positiivsed arvud, mis on väiksemad kui 22, s.o. see järjestus on piiratud. Weierstrassi teoreemi järgi (vt § 30) kui jada on kasvav ja piiratud, siis see koondub. Pealegi teame §-st 30, et kui jada koondub, siis ainult ühe piirini. Seda ühtset piirmäära lepiti kokku käsitleda arvavaldise väärtusena. Ja see pole oluline, et arvavaldise 2 ligikaudset väärtust on väga raske leida; on oluline, et see oleks konkreetne arv (lõppude lõpuks ei kartnud me öelda, et see on näiteks ratsionaalse võrrandi juur, ![]() trigonomeetrilise võrrandi juur, mõtlemata sellele, mis need arvud täpselt on:
trigonomeetrilise võrrandi juur, mõtlemata sellele, mis need arvud täpselt on: ![]()
Niisiis, saime teada, mis tähenduse matemaatikud sümbolile 2 ^ andsid. Samamoodi saab määrata, mis on ja mis üldiselt on a a, kus a on irratsionaalne arv ja a > 1.
Aga mis siis, kui 0<а <1? Как вычислить, например, ? Самым естественным способом: считать, что свести вычисления к случаю, когда основание степени больше 1.
Nüüd saame rääkida mitte ainult suvaliste ratsionaalsete astendajatega võimsustest, vaid ka suvaliste reaalastendajatega võimsustest. On tõestatud, et mistahes reaalastendajatega kraadidel on kõik tavalised kraadiomadused: kraadide korrutamisel samade alustega astendajad liidetakse, jagamisel lahutatakse, astme tõstmisel astmeni korrutatakse jne. . Kuid kõige tähtsam on see, et nüüd saame rääkida funktsioonist y-ax, mis on defineeritud kõigi reaalarvude hulgal.
Pöördume tagasi funktsiooni y \u003d 2 x juurde, koostame selle graafiku. Selleks koostame funktsiooni väärtuste tabeli \u200b\u200d 2 x:

Märgime punktid koordinaattasandil (joon. 194), need joonistavad välja teatud joone, joonestage see (joon. 195).

Funktsiooni omadused y - 2 x:
1)
2) ei ole paaris ega paaritu; 248
3) suureneb;
5) ei oma suurimaid ega väikseimaid väärtusi;
6) pidev;
7)
8) kumer allapoole.
Funktsiooni y-2 x loetletud omaduste ranged tõestused on antud kõrgema matemaatika käigus. Mõnda neist omadustest me ühel või teisel määral varem käsitlesime, osa neist on selgelt näidatud konstrueeritud graafikuga (vt joonis 195). Näiteks funktsiooni paarsuse või veidruse puudumine on geomeetriliselt seotud graafiku sümmeetria puudumisega vastavalt y-telje või alguspunkti suhtes.
Igal funktsioonil kujul y=a x, kus a >1, on sarnased omadused. Joonisel fig. 196 ühes koordinaatsüsteemis koostatakse, funktsioonide y=2 x, y=3 x, y=5 x graafikud.
Nüüd kaalume funktsiooni , koostame selle jaoks väärtuste tabeli:

Märgime punktid koordinaattasandile (joonis 197), need visandavad teatud joone, tõmmake see (joonis 198).

Funktsiooni omadused
1)
2) ei ole paaris ega paaritu;
3) väheneb;
4) ülalt piiramata, alt piiratud;
5) puuduvad suurimad ega väikseimad väärtused;
6) pidev;
7)
8) kumer allapoole.
Mis tahes funktsioon kujul y \u003d a x, kus O<а <1. На рис. 200 в одной системе координат построены графики функций ![]()
Pange tähele: funktsioonigraafikud ![]() need. y \u003d 2 x, sümmeetriline y-telje suhtes (joonis 201). See on üldlause (vt § 13) tagajärg: funktsioonide y = f(x) ja y = f(-x) graafikud on y-telje suhtes sümmeetrilised. Samamoodi on funktsioonide y \u003d 3 x ja graafikud
need. y \u003d 2 x, sümmeetriline y-telje suhtes (joonis 201). See on üldlause (vt § 13) tagajärg: funktsioonide y = f(x) ja y = f(-x) graafikud on y-telje suhtes sümmeetrilised. Samamoodi on funktsioonide y \u003d 3 x ja graafikud

Öeldut kokku võttes anname eksponentsiaalfunktsiooni definitsiooni ja toome välja selle olulisemad omadused.
Definitsioon. Vaatefunktsiooni nimetatakse eksponentsiaalfunktsiooniks.
Eksponentfunktsiooni y \u003d a x peamised omadused

Funktsiooni y \u003d a x graafik a> 1 korral on näidatud joonisel fig. 201 ja 0 jaoks<а < 1 - на рис. 202.
Joonisel fig. 201 või 202 nimetatakse eksponendiks. Tegelikult nimetavad matemaatikud eksponentsiaalfunktsiooni ennast tavaliselt y = a x. Seega kasutatakse terminit "eksponent" kahes tähenduses: nii eksponentsiaalfunktsiooni nime kui ka eksponentsiaalfunktsiooni graafiku nimetuse jaoks. Tavaliselt on tähenduses selge, kas me räägime eksponentsiaalfunktsioonist või selle graafikust.
Pöörake tähelepanu eksponentsiaalfunktsiooni y \u003d ax graafiku geomeetrilisele tunnusele: x-telg on graafiku horisontaalne asümptoot. Tõsi, seda väidet täpsustatakse tavaliselt järgmiselt.
X-telg on funktsiooni graafiku horisontaalne asümptoot

Teisisõnu

Esimene oluline märkus. Koolilapsed ajavad sageli segi mõisted: võimsusfunktsioon, eksponentsiaalfunktsioon. Võrdlema:
Need on näited võimsusfunktsioonidest; ![]()
on eksponentsiaalfunktsioonide näited.
Üldiselt on y \u003d x r, kus r on konkreetne arv, astmefunktsioon (argument x sisaldub astme aluses);
y \u003d a", kus a on konkreetne arv (positiivne ja erineb 1-st), on eksponentsiaalne funktsioon (argument x sisaldub eksponendis).
Ründavat "eksootilist" funktsiooni nagu y = x ei peeta eksponentsiaalseks ega võimsusseaduseks (seda nimetatakse mõnikord eksponentsiaalvõimsuse funktsiooniks).
Teine oluline märkus. Tavaliselt ei arvestata eksponentsiaalfunktsiooni, mille alus on a = 1 või alus a, mis rahuldab ebavõrdsust a<0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0ja a Fakt on see, et kui a \u003d 1, siis mis tahes väärtuse x korral on võrdsus Ix \u003d 1 tõene. Seega taandub eksponentsiaalne funktsioon y \u003d a "a \u003d 1" konstantseks funktsiooniks y \ u003d 1 - see pole huvitav. Kui a \u003d 0, siis 0x \u003d 0 x mis tahes positiivse väärtuse korral, st saame funktsiooni y \u003d 0, mis on määratletud x\u003e 0 jaoks - see pole samuti huvitav.<0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках.
Enne näidete lahendamise juurde asumist märgime, et eksponentsiaalfunktsioon erineb oluliselt kõigist seni uuritud funktsioonidest. Uue objekti põhjalikuks uurimiseks peate seda kaaluma erinevate nurkade alt, erinevates olukordades, nii et näiteid on palju.
Näide 1
Lahendus, a) Olles joonistanud funktsioonide y \u003d 2 x ja y \u003d 1 graafikud ühte koordinaatsüsteemi, märkame (joonis 203), et neil on üks ühine punkt (0; 1). Seega on võrrandil 2x = 1 üks juur x = 0.
Seega saime võrrandist 2x = 2° x = 0.
b) Olles koostanud funktsioonide y \u003d 2 x ja y \u003d 4 graafikud ühes koordinaatsüsteemis, märkame (joonis 203), et neil on üks ühine punkt (2; 4). Seega on võrrandil 2x = 4 üks juur x = 2.
Niisiis, võrrandist 2 x \u003d 2 2 saime x \u003d 2.
c) ja d) Samadele kaalutlustele tuginedes järeldame, et võrrandil 2 x \u003d 8 on üks juur ja selle leidmiseks ei pruugi vastavate funktsioonide graafikuid koostada;
on selge, et x=3, kuna 2 3 =8. Samamoodi leiame võrrandi ainsa juure

Seega saime võrrandist 2x = 2 3 x = 3 ja võrrandist 2 x = 2 x saime x = -4.
e) Funktsiooni y \u003d 2 x graafik asub funktsiooni y \u003d 1 graafiku kohal x\u003e 0 korral - see on hästi loetav jooniselt fig. 203. Seega on võrratuse 2x > 1 lahendus intervall
f) Funktsiooni y \u003d 2 x graafik asub funktsiooni y \u003d 4 graafiku all punktis x<2 - это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток
Tõenäoliselt märkasite, et kõigi näite 1 lahendamisel tehtud järelduste aluseks oli funktsiooni y \u003d 2 x monotoonsuse (suurenemise) omadus. Sarnane arutluskäik võimaldab meil kontrollida kahe järgmise teoreemi paikapidavust.
Lahendus. Saate toimida järgmiselt: koostage funktsiooni y-3 x graafik, seejärel venitage seda x-teljelt koefitsiendiga 3 ja tõstke saadud graafikut 2 mõõtkava ühiku võrra üles. Kuid mugavam on kasutada asjaolu, et 3- 3* \u003d 3 * + 1, ja seetõttu joonistada funktsioon y \u003d 3 x * 1 + 2.

Liigume edasi, nagu oleme sellistel juhtudel korduvalt teinud, abikoordinaatide süsteemi, mille alguspunkt on punktis (-1; 2) - punktiirjooned x = - 1 ja 1x = 2 joonisel fig. 207. "Kinnitame" funktsiooni y=3* uude koordinaatsüsteemi. Selleks valime funktsiooni kontrollpunktid ![]() , kuid me ehitame need mitte vanasse, vaid uude koordinaatsüsteemi (need punktid on märgitud joonisel 207). Seejärel konstrueerime punktide kaupa eksponendi – see on vajalik graaf (vt joonis 207).
, kuid me ehitame need mitte vanasse, vaid uude koordinaatsüsteemi (need punktid on märgitud joonisel 207). Seejärel konstrueerime punktide kaupa eksponendi – see on vajalik graaf (vt joonis 207).
Antud funktsiooni suurima ja väikseima väärtuse leidmiseks segmendil [-2, 2] kasutame seda, et antud funktsioon kasvab ja seetõttu võtab see oma väikseimad ja suurimad väärtused vastavalt vasakul ja segmendi paremad otsad.
Niisiis:
![]()
Näide 4 Lahendage võrrand ja võrratused:
Lahendus, a) Koostame funktsioonide y=5* ja y=6-x graafikud ühes koordinaatsüsteemis (joonis 208). Nad ristuvad ühes punktis; joonise järgi otsustades on see punkt (1; 5). Kontroll näitab, et tegelikult punkt (1; 5) rahuldab nii võrrandit y = 5* kui ka võrrandit y=6x. Selle punkti abstsiss on antud võrrandi ainus juur.
Seega on võrrandil 5 x = 6-x üks juur x = 1.
b) ja c) Eksponent y-5x asub sirge y=6-x kohal, kui x>1, - see on selgelt näha joonisel fig. 208. Seega võib võrratuse 5*>6-x lahendi kirjutada järgmiselt: x>1. Ja ebavõrdsuse lahendus 5x<6 - х можно записать так: х < 1.
Vastus: a) x = 1; b)x>1; c)x<1.

Näide 5 Antud funktsioon ![]() Tõesta seda
Tõesta seda ![]()
Lahendus. Tingimuste järgi Meil on.
EKSPONENTSIAAL- JA LOGARITMILISED FUNKTSIOONID VIII
§ 179 Eksponentfunktsiooni põhiomadused
Selles osas uurime eksponentsiaalfunktsiooni põhiomadusi
y = a x (1)
Tuletage see meelde allpool a valemis (1) peame silmas mis tahes fikseeritud positiivset arvu, mis ei ole 1.
Vara 1. Eksponentfunktsiooni domeen on kõigi reaalarvude hulk.
Tõepoolest, positiivseks a väljendus a x defineeritud mis tahes reaalarvu jaoks X .
Vara 2. Eksponentfunktsioon võtab ainult positiivseid väärtusi.
Tõepoolest, kui X > 0, siis, nagu on tõendatud §-s 176,
a x > 0.
Kui X <. 0, то
a x =
kus - X juba suurem kui null. Sellepärast a - x > 0. Aga siis
a x = > 0.
Lõpuks kl X = 0
a x = 1.
Eksponentfunktsiooni 2. omadusel on lihtne graafiline tõlgendus. See seisneb selles, et selle funktsiooni graafik (vt joonised 246 ja 247) asub täielikult x-telje kohal.

Vara 3. Kui a a >1, siis kl X > 0 a x > 1, ja kell X < 0 a x < 1. Kui a < 1, тoh, vastupidi, X > 0 a x < 1, ja kell X < 0 a x > 1.
See eksponentsiaalfunktsiooni omadus võimaldab ka lihtsat geomeetrilist tõlgendamist. Kell a > 1 (joon. 246) kõverad y = a x asub joone kohal juures = 1 at X > 0 ja allapoole sirgjoont juures = 1 at X < 0.
Kui a < 1 (рис. 247), то, наоборот, кривые y = a x asub joone all juures = 1 at X > 0 ja sellest sirgest kõrgemal punktis X < 0.
Andkem 3. omaduse täpne tõend. Lase a > 1 ja X on suvaline positiivne arv. Näitame seda
a x > 1.
Kui number X ratsionaalne ( X = m / n ), siis a x = a m / n = n √a m .
Kuna a > 1, siis a m > 1, kuid ühest suurema arvu juur on ilmselt samuti suurem kui 1.
Kui a X irratsionaalne, siis on olemas positiivsed ratsionaalarvud X" ja X" , mis toimivad arvu kümnendarvuna x :
X"< х < х" .
Aga siis, kraadi määratluse järgi irratsionaalse astendajaga
a x" < a x < a x"" .
Nagu ülal näidatud, number a x" rohkem kui üks. Seetõttu number a x , rohkem kui a x" , peab samuti olema suurem kui 1,
Niisiis, me oleme seda näidanud a >1 ja suvaliselt positiivne X
a x > 1.
Kui number X oli negatiivne, siis oleksime
a x =
kus on number X oleks positiivne. Sellepärast a - x > 1. Seetõttu
a x = < 1.
Seega, kl a > 1 ja suvaliselt negatiivne x
a x < 1.
Juhtum, kui 0< a < 1, легко сводится к уже рассмотренному случаю. Учащимся предлагается убедиться в этом самостоятельно.
Vara 4. Kui x = 0, siis olenemata a a x =1.
See tuleneb nullkraadi definitsioonist; nullist erineva arvu nullaste on võrdne 1-ga. Graafiliselt väljendub see omadus selles, et mis tahes arvu korral a kõver juures = a x (vt joonis 246 ja 247) ristub teljega juures punktis 1. ordinaatiga.
Vara 5. Kell a >1 eksponentsiaalne funktsioon = a x kasvab monotoonselt ja a jaoks < 1 - monotoonselt väheneb.
See omadus võimaldab ka lihtsat geomeetrilist tõlgendust.
Kell a > 1 (joonis 246) kõver juures = a x kasvuga X tõuseb aina kõrgemale ja kõrgemale ning a < 1 (рис. 247) - опускается все ниже и ниже.
Andkem 5. omaduse täpne tõend.
Lase a > 1 ja X 2 > X üks . Näitame seda
a x 2 > a x 1
Kuna X 2 > X 1., siis X 2 = X 1 + d , kus d on mingi positiivne arv. Sellepärast
a x 2 - a x 1 = a x 1 + d - a x 1 = a x 1 (a d - 1)
Eksponentfunktsiooni 2. omaduse järgi a x 1 > 0. Alates d > 0, siis eksponentsiaalfunktsiooni 3. omaduse järgi a d > 1. Toote mõlemad tegurid a x 1 (a d - 1) on positiivsed, seega on see toode ise positiivne. Tähendab, a x 2 - a x 1 > 0 või a x 2 > a x 1 , mida tuli tõestada.
Niisiis, kl a > 1 funktsioon juures = a x suureneb monotoonselt. Samamoodi on tõestatud, et a < 1 функция juures = a x väheneb monotoonselt.
Tagajärg. Kui sama positiivse arvu kaks astet, mis ei ole 1, on võrdsed, on ka nende eksponendid võrdsed.
Teisisõnu, kui
a b = a c (a > 0 ja a =/= 1),
b = c .
Tõepoolest, kui numbrid b ja Koos ei olnud funktsiooni monotoonsuse tõttu võrdsed juures = a x enamik neist vastaks a >1 on suurem ja juures a < 1 меньшее значение этой функции. Таким образом, было бы или a b > a c , või a b < a c . Mõlemad on tingimusega vastuolus a b = a c . Jääb üle tunnistada, et b = c .
Vara 6. Kui a > 1, siis argumendi piiramatu kasvuga X (X -> ∞ ) funktsiooni väärtused juures = a x kasvab ka lõputult (juures -> ∞ ). Vaidluse piiramatu vähenemisega X (X -> -∞ ) selle funktsiooni väärtused kalduvad nulli, jäädes samas positiivseks (juures->0; juures > 0).
Võttes arvesse funktsiooni ülaltoodud monotoonsust juures = a x , võime öelda, et vaadeldaval juhul on funktsioon juures = a x suureneb monotoonselt 0-st kuni ∞ .
Kui a 0 <a < 1, siis argumendi x (x -> ∞) piiramatu suurenemisega kipuvad funktsiooni y \u003d a x väärtused nulli jääma, jäädes positiivseks (juures->0; juures > 0). Argumendi x piiramatu vähenemisega (X -> -∞ ) selle funktsiooni väärtused kasvavad lõputult (juures -> ∞ ).
Funktsiooni monotoonsuse tõttu y = a x võime öelda, et antud juhul funktsioon juures = a x väheneb monotoonselt alates ∞ 0-le.
Eksponentfunktsiooni 6. omadus kajastub selgelt joonistel 246 ja 247. Me ei hakka seda rangelt tõestama.
Peame ainult määrama eksponentsiaalfunktsiooni vahemiku y = a x (a > 0, a =/= 1).
Eespool tõestasime, et funktsioon y = a x võtab ainult positiivseid väärtusi ja kas suureneb monotoonselt 0-st ∞ (at a > 1) või väheneb monotoonselt alates ∞ 0-le (0< a <. 1). Однако остался невыясненным следующий вопрос: не претерпевает ли функция y = a x kui muudate hüppeid? Kas see eeldab positiivseid väärtusi? Sellele küsimusele vastatakse positiivselt. Kui a > 0 ja a =/= 1, siis olenemata sellest, milline on positiivne arv juures 0 tuleb leida X 0, selline
a x 0 = juures 0 .
(Funktsiooni monotoonsuse tõttu y = a x määratud väärtus X 0 oleks muidugi ainuke.)
Selle fakti tõestus ei kuulu meie programmi raamidesse. Selle geomeetriline tõlgendus on mis tahes positiivse väärtuse puhul juures 0 funktsiooni graafik y = a x peab ristuma joonega juures = juures 0 ja pealegi ainult ühes punktis (joonis 248).

Sellest saame teha järgmise järelduse, mille sõnastame omaduse 7 kujul.
Vara 7. Eksponentfunktsiooni y \u003d a x muutumisala (a > 0, a =/= 1)on kõigi positiivsete arvude hulk.
Harjutused
1368. Leidke järgmiste funktsioonide domeenid:
1369. Milline antud arvudest on suurem kui 1 ja milline väiksem kui 1:

1370. Millise eksponentsiaalfunktsiooni omaduse põhjal saab seda väita
a) (5/7) 2,6 > (5/7) 2,5; b) (4/3) 1,3 > (4/3) 1,2
1371. Milline arv on suurem:
a) π - √3 või (1 / π ) - √3; c) (2/3) 1 + √6 või (2/3) √2 + √5 ;
b) ( π / 4) 1 + √3 või ( π / 4) 2; d) (√3 ) √2 - √5 või (√3) √3 - 2 ?
1372. Kas võrratused on samaväärsed:
1373. Mida saab öelda arvude kohta X ja juures , kui a x = ja y , kus a kas antud positiivne arv?
1374. 1) Kas see on võimalik funktsiooni kõigi väärtuste hulgas juures = 2x esile:
2) Kas see on võimalik kõigi funktsiooni väärtuste hulgas juures = 2 | x| esile:
a) suurim väärtus; b) väikseim väärtus?
