הגדרה וגרף של פונקציה אקספוננציאלית. שיעור "פונקציה אקספוננציאלית, תכונותיה וגרף

תחילה אנו מציגים את ההגדרה של פונקציה מעריכית.

הפונקציה המעריכית $f\left(x\right)=a^x$, כאשר $a >1$.

הבה נציג את המאפיינים של הפונקציה המעריכית, עבור $a >1$.

\\[אין שורשים\] \

צומת עם צירי קואורדינטות. הפונקציה אינה חותכת את ציר $Ox$, אלא חותכת את ציר $Oy$ בנקודה $(0,1)$.

$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$

\\[אין שורשים\] \

גרף (איור 1).

איור 1. גרף של הפונקציה $f\left(x\right)=a^x,\ עבור \ a >1$.

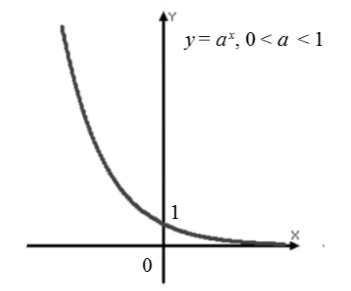
הפונקציה המעריכית $f\left(x\right)=a^x$, כאשר $0

הבה נציג את המאפיינים של הפונקציה המעריכית, עבור $0

תחום ההגדרה הוא כל המספרים הממשיים.

$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- הפונקציה אינה זוגית ואינה.

$f(x)$ הוא רציף בכל תחום ההגדרה.

טווח הערך הוא המרווח $(0,+\infty)$.

$f"(x)=\left(a^x\right)"=a^xlna$

\ \[אין שורשים\] \ \[אין שורשים\] \

הפונקציה קמורה בכל תחום ההגדרה.

התנהגות בקצות ההיקף:

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]

גרף (איור 2).

דוגמה למשימה לבניית פונקציה אקספוננציאלית

חקור ושרטט את הפונקציה $y=2^x+3$.

הַחְלָטָה.

בואו נערוך מחקר על הדוגמה של התכנית לעיל:

תחום ההגדרה הוא כל המספרים הממשיים.

$f\left(-x\right)=2^(-x)+3$ -- הפונקציה אינה זוגית ואינה.

$f(x)$ הוא רציף בכל תחום ההגדרה.

טווח הערך הוא המרווח $(3,+\infty)$.

$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$

הפונקציה גדלה על פני כל תחום ההגדרה.

$f(x)\ge 0$ על כל תחום ההגדרה.

צומת עם צירי קואורדינטות. הפונקציה אינה חותכת את ציר $Ox$, אלא חותכת את ציר $Oy$ בנקודה ($0,4)$

$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$

הפונקציה קמורה בכל תחום ההגדרה.

התנהגות בקצות ההיקף:

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\]

גרף (איור 3).

איור 3. גרף של הפונקציה $f\left(x\right)=2^x+3$

פונקציה מעריכית

פונקציה של הצורה y = a איקס , כאשר a גדול מאפס ו-a אינו שווה לאחד נקראת פונקציה מעריכית. המאפיינים העיקריים של הפונקציה האקספוננציאלית:

1. התחום של הפונקציה המעריכית יהיה קבוצת המספרים הממשיים.

2. הטווח של הפונקציה המעריכית יהיה קבוצת כל המספרים הממשיים החיוביים. לפעמים קבוצה זו מסומנת כ-R+ לקיצור.

3. אם בפונקציה אקספוננציאלית הבסיס a גדול מאחד, אזי הפונקציה תגדל על פני כל תחום ההגדרה. אם הפונקציה המעריכית עבור הבסיס a עומדת בתנאי הבא 0

4. כל המאפיינים הבסיסיים של תארים יהיו תקפים. המאפיינים העיקריים של התארים מיוצגים על ידי השוויון הבא:

א איקס *א y = א (x+y) ;

(א איקס )/(א y ) = א (x-y) ;

(א*ב) איקס = (א איקס )*(א y );

(א/ב) איקס = א איקס /ב איקס ;

(א איקס ) y = א (x*y) .

השוויון הזה יהיה תקף עבור כל הערכים האמיתיים של x ו-y.

5. הגרף של הפונקציה המעריכית עובר תמיד דרך הנקודה עם קואורדינטות (0;1)

6. תלוי אם הפונקציה המעריכית עולה או יורדת, הגרף שלה יהיה אחד משני סוגים.

האיור הבא מציג גרף של פונקציה אקספוננציאלית הולכת וגדלה: a>0.

האיור הבא הוא גרף של פונקציה מעריכית יורדת: 0

גם הגרף של הפונקציה האקספוננציאלית ההולכת וגדלה וגם הגרף של הפונקציה המעריכית היורדת, לפי התכונה המתוארת בפסקה החמישית, עוברים דרך הנקודה (0; 1).

7. לפונקציה אקספוננציאלית אין נקודות קיצון, כלומר, במילים אחרות, אין לה נקודות מינימום ומקסימום של הפונקציה. אם ניקח בחשבון את הפונקציה על קטע מסוים, אז הפונקציה תיקח את ערכי המינימום והמקסימום בקצה המרווח הזה.

8. הפונקציה אינה זוגית או אי זוגית. פונקציה אקספוננציאלית היא פונקציה כללית. ניתן לראות זאת גם מהגרפים, אף אחד מהם אינו סימטרי לא לגבי ציר Oy ולא לגבי המקור.

לוֹגָרִיתְם

לוגריתמים תמיד נחשבו לנושא קשה בקורס המתמטיקה בבית הספר. ישנן הגדרות רבות ושונות ללוגריתם, אך משום מה רוב ספרי הלימוד משתמשים במורכבות והמצערות שבהן.

נגדיר את הלוגריתם בצורה פשוטה וברורה. בואו ניצור טבלה בשביל זה:

אז יש לנו כוחות של שניים. אם אתה לוקח את המספר מהשורה התחתונה, אתה יכול בקלות למצוא את הכוח שאליו אתה צריך להעלות שתיים כדי לקבל את המספר הזה. לדוגמה, כדי לקבל 16, אתה צריך להעלות שניים לחזקה רביעית. וכדי לקבל 64, אתה צריך להעלות שניים לחזקה השישית. ניתן לראות זאת מהטבלה.

ועכשיו - למעשה, ההגדרה של הלוגריתם:

הַגדָרָה

לוֹגָרִיתְםבסיס a מארגומנט x הוא הכוח שאליו יש להעלות את המספרא כדי לקבל את המספראיקס.

יִעוּד

log a x = b
כאשר a הוא הבסיס, x הוא הארגומנט, ב מהו בדיוק הלוגריתם.

לדוגמה, 2 3 = 8 ⇒ log 2 8 = 3 (לוגריתם הבסיס 2 של 8 הוא שלוש כי 2 3 = 8). אפשר גם לרשום 2 64 = 6, כי 2 6 = 64.

הפעולה של מציאת הלוגריתם של מספר לבסיס נתון נקראתלוֹגָרִיתְם . אז בואו נוסיף שורה חדשה לטבלה שלנו:

למרבה הצער, לא כל הלוגריתמים נחשבים כל כך בקלות. לדוגמה, נסה למצוא את לוג 2 5. המספר 5 לא נמצא בטבלה, אבל ההיגיון מכתיב שהלוגריתם יהיה איפשהו על הקטע. כי 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

מספרים כאלה נקראים אי-רציונליים: המספרים שאחרי הנקודה העשרונית יכולים להיכתב ללא הגבלה, והם לעולם לא חוזרים על עצמם. אם הלוגריתם מתברר כלא רציונלי, עדיף להשאיר אותו כך: יומן 2 5, יומן 3 8, יומן 5 100.

חשוב להבין שהלוגריתם הוא ביטוי בעל שני משתנים (בסיס וארגומנט). בהתחלה, אנשים רבים מבלבלים היכן נמצא הבסיס והיכן הטיעון. כדי למנוע אי הבנות מעצבנות, פשוט תסתכל על התמונה:

לפנינו לא יותר מהגדרת הלוגריתם. זכור: הלוגריתם הוא חזקה , שאליו אתה צריך להעלות את הבסיס כדי לקבל את הטיעון.זה הבסיס שמורם לעוצמה - בתמונה הוא מודגש באדום. מסתבר שהבסיס תמיד בתחתית! את הכלל הנפלא הזה אני מספר לתלמידים שלי כבר בשיעור הראשון - ואין בלבול.

הבנו את ההגדרה - נותר ללמוד איך לספור לוגריתמים, כלומר. להיפטר מהסימן "יומן". מלכתחילה, נציין זאת שתי עובדות חשובות נובעות מההגדרה:

הארגומנט והבסיס חייבים תמיד להיות גדולים מאפס. הדבר נובע מהגדרת התואר על ידי מעריך רציונלי, שאליו מצטמצמת הגדרת הלוגריתם.

הבסיס חייב להיות שונה מאחדות, שכן יחידה לכל כוח היא עדיין יחידה.בגלל זה, השאלה "לאיזה כוח צריך להעלות אחד כדי לקבל שניים" היא חסרת משמעות. אין תואר כזה!

הגבלות כאלהשקוראים לו טווח חוקי(ODZ). מסתבר שה-ODZ של הלוגריתם נראה כך: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

שים לב ש ללא הגבלה על המספרב (ערך לוגריתם) אינו חופף. לדוגמה, הלוגריתם עשוי להיות שלילי: log 2 0.5 = −1, כי 0.5 = 2-1.

עם זאת, כעת אנו שוקלים רק ביטויים מספריים, שבהם אין צורך לדעת את ה-ODZ של הלוגריתם. כל ההגבלות כבר נלקחו בחשבון על ידי מהדרים של הבעיות. אבל כאשר משוואות לוגריתמיות ואי-שוויון נכנסות לפעולה, דרישות ה-DHS יהפכו לחובה. אכן, בבסיס ובטיעון יכולות להיות קונסטרוקציות חזקות מאוד, שאינן בהכרח תואמות את ההגבלות הנ"ל.

עַכשָׁיו לשקול את הכללי סכימה לחישוב לוגריתמים. זה מורכב משלושה שלבים:

שלח קרן a וארגומנט x ככוח עם הבסיס הקטן ביותר האפשרי גדול מאחד. על הדרך, עדיף להיפטר משברים עשרוניים;

החליטו על משתנהמשוואת b: x = a b ;

מספר שהתקבל b תהיה התשובה.

זה הכל! אם הלוגריתם יתברר כלא רציונלי, זה ייראה כבר בשלב הראשון. הדרישה שהבסיס יהיה גדול מאחד רלוונטית מאוד: זה מקטין את הסבירות לטעות ומפשט מאוד את החישובים. בדומה לשברים עשרוניים: אם תמיר אותם מיד לשברים רגילים, יהיו הרבה פעמים פחות שגיאות.

בוא נראה איך תכנית זו פועלת עם דוגמאות ספציפיות:

חשב את הלוגריתם: log 5 25

בואו נציג את הבסיס והארגומנט בחזקת חמש: 5 = 5 1 ; 25 = 52;

בואו ניצור ונפתור את המשוואה:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;

קיבל תשובה: 2.

חשב את הלוגריתם:

בואו נציג את הבסיס והארגומנט בחזקת שלוש: 3 = 3 1 ; 1/81 \u003d 81 -1 \u003d (3 4) -1 \u003d 3 -4;

בואו ניצור ונפתור את המשוואה:

קיבלתי את התשובה: -4.

−4

חשב את הלוגריתם: log 4 64

הבה נציג את הבסיס ואת הארגומנט בחזקת שתיים: 4 = 2 2 ; 64 = 26;

בואו ניצור ונפתור את המשוואה:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2b = 6 ⇒ b = 3;

קיבל תשובה: 3.

חשב את הלוגריתם: יומן 16 1

הבה נציג את הבסיס ואת הארגומנט בחזקת שתיים: 16 = 2 4 ; 1 = 20;

בואו ניצור ונפתור את המשוואה:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4b = 0 ⇒ b = 0;

התקבלה תגובה: 0.

חשב את הלוגריתם: log 7 14

הבה נציג את הבסיס ואת הארגומנט בחזקת שבע: 7 = 7 1 ; 14 אינו מיוצג בחזקת שבע, כי 7 1< 14 < 7 2 ;

מהפסקה הקודמת עולה שהלוגריתם אינו נחשב;

התשובה היא ללא שינוי: יומן 7 14.

יומן 7 14

הערה קטנה לגבי הדוגמה האחרונה. איך לוודא שמספר אינו חזקת מדוייקת של מספר אחר? פשוט מאוד - פשוט לפרק אותו לגורמים ראשוניים. אם יש לפחות שני גורמים ברורים בהרחבה, המספר אינו כוח מדויק.

גלה אם החזקות המדויקות של המספר הן: 8; 48; 81; 35; ארבעה עשר.

8 \u003d 2 2 2 \u003d 2 3 - התואר המדויק, מכיוון יש רק מכפיל אחד;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 אינו כוח מדויק כי ישנם שני גורמים: 3 ו-2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - תואר מדויק;
35 = 7 5 - שוב לא תואר מדויק;
14 \u003d 7 2 - שוב לא תואר מדויק;

8, 81 - תואר מדויק; 48, 35, 14 - לא.

שימו לב גם שהמספרים הראשוניים עצמם הם תמיד כוחות מדויקים של עצמם.

לוגריתם עשרוני

כמה לוגריתמים כל כך נפוצים שיש להם שם וייעוד מיוחדים.

הַגדָרָה

לוגריתם עשרונימארגומנט x הוא הלוגריתם לבסיס 10, כלומר. העוצמה שאליה אתה צריך להעלות את המספר 10 כדי לקבל את המספראיקס.

יִעוּד

lg x

לדוגמה, יומן 10 = 1; log 100 = 2; lg 1000 = 3 - וכו'.

מעתה ואילך, כאשר מופיע ביטוי כמו "מצא lg 0.01" בספר הלימוד, דעו שזו לא שגיאת הקלדה. זהו הלוגריתם העשרוני. עם זאת, אם אתה לא רגיל לייעוד כזה, אתה תמיד יכול לכתוב אותו מחדש:
log x = log 10 x

כל מה שנכון ללוגריתמים רגילים נכון גם לעשרונים.

לוגריתם טבעי

יש לוגריתם אחר שיש לו סימון משלו. במובן מסוים, זה אפילו יותר חשוב מהעשרוני. זהו הלוגריתם הטבעי.

הַגדָרָה

לוגריתם טבעימארגומנט x הוא הלוגריתם הבסיסיה , כלומר העוצמה שאליה יש להעלות את המספרה כדי לקבל את המספראיקס.

יִעוּד

ln x

רבים ישאלו: מהו המספר e? זהו מספר אי-רציונלי, לא ניתן למצוא ולכתוב את ערכו המדויק. הנה רק המספרים הראשונים:
e = 2.718281828459...

לא נתעמק מהו המספר הזה ומדוע הוא נחוץ. רק תזכור כי ה הוא הבסיס של הלוגריתם הטבעי:
ב x = log e x

לפיכך ln e = 1; log e 2 = 2; ב e 16 = 16 - וכו'. מצד שני, ln 2 הוא מספר אי רציונלי. באופן כללי, הלוגריתם הטבעי של כל מספר רציונלי הוא אי רציונלי. מלבד, כמובן, אחדות: ln 1 = 0.

עבור לוגריתמים טבעיים, כל הכללים שנכונים ללוגריתמים רגילים תקפים.

מאפיינים בסיסיים של לוגריתמים

לוגריתמים, כמו כל מספר, ניתן להוסיף, לגרוע ולהמיר בכל דרך אפשרית. אבל מכיוון שהלוגריתמים אינם מספרים רגילים לגמרי, יש כאן כללים, הנקראים מאפיינים בסיסיים.

חוקים אלו חייבים להיות ידועים - לא ניתן לפתור בעיה לוגריתמית רצינית בלעדיהם. בנוסף, יש מעט מאוד מהם - הכל ניתן ללמוד ביום אחד. אז בואו נתחיל.

חיבור וחיסור של לוגריתמים

שקול שני לוגריתמים עם אותו בסיס: log a x ויומן a y . לאחר מכן ניתן להוסיף ולהחסיר אותם, ו:

עֵץ a x + יומןא y = יומןא ( איקס · y );

עֵץ a x −לוגא y = יומןא ( איקס : y ).

כך, סכום הלוגריתמים שווה ללוגריתם של המכפלה, וההבדל הוא הלוגריתם של המנה.שימו לב: נקודת המפתח כאן היא אותם בסיסים. אם הבסיסים שונים, הכללים האלה לא עובדים!

נוסחאות אלו יעזרו לך לחשב את הביטוי הלוגריתמי גם כאשר חלקיו הבודדים אינם נחשבים (ראה את השיעור " "). תסתכל על הדוגמאות - וראה:

מצא את הערך של הביטוי: log 6 4 + log 6 9.

מכיוון שהבסיסים של הלוגריתמים זהים, אנו משתמשים בנוסחת הסכום:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

מצא את הערך של הביטוי: log 2 48 − log 2 3.

הבסיסים זהים, אנו משתמשים בנוסחת ההבדל:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

מצא את הערך של הביטוי: log 3 135 − log 3 5.

שוב, הבסיסים זהים, אז יש לנו:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

כפי שניתן לראות, הביטויים המקוריים מורכבים מלוגריתמים "רעים", שאינם נחשבים בנפרד. אבל לאחר טרנספורמציות מסתבר מספרים נורמליים למדי. בדיקות רבות מבוססות על עובדה זו. כן, השליטה הזו - ביטויים דומים במלוא הרצינות (לפעמים - כמעט ללא שינויים) מוצעים בבחינה.

הסרת המעריך מהלוגריתם

עכשיו בואו נסבך מעט את המשימה. מה אם יש תואר בבסיס או בארגומנט של הלוגריתם? לאחר מכן ניתן להוציא את המעריך של תואר זה מהסימן של הלוגריתם לפי הכללים הבאים:

קל לראות שהכלל האחרון עוקב אחר השניים הראשונים שלהם. אבל עדיף בכל זאת לזכור - במקרים מסוימים זה יקטין משמעותית את כמות החישובים.

כמובן כל הכללים האלה הגיוניים אם הלוגריתם של ODZ מתקיים: a > 0, a ≠ 1, x > 0 אתה יכול להזין את המספרים לפני הסימן של הלוגריתם לתוך הלוגריתם עצמו. זה מה שנדרש לרוב.

מצא את הערך של הביטוי: log 7 49 6 .

בואו נפטר מהדרגה בטיעון לפי הנוסחה הראשונה:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

מצא את הערך של הביטוי:

שימו לב שהמכנה הוא לוגריתם שהבסיס והארגומנט שלו הם בחזקות מדויקות: 16 = 2 4 ; 49 = 72. יש לנו:

אני חושב שהדוגמה האחרונה דורשת הבהרה. לאן נעלמו הלוגריתמים? עד הרגע האחרון אנחנו עובדים רק עם המכנה. הם הציגו את הבסיס והטיעון של הלוגריתם שעומד שם בצורה של מעלות והוציאו את האינדיקטורים - הם קיבלו שבר של "שלוש קומות".

עכשיו בואו נסתכל על השבר העיקרי. למונה ולמכנה יש אותו מספר: log 2 7. מכיוון שלוג 2 7 ≠ 0, נוכל לצמצם את השבר - 2/4 יישאר במכנה. לפי כללי החשבון ניתן להעביר את הארבעה למונה, מה שנעשה. התוצאה היא התשובה: 2.

מעבר לקרן חדשה

כשדיברתי על הכללים לחיבור והפחתה של לוגריתמים, הדגשתי במיוחד שהם עובדים רק עם אותם בסיסים. מה אם הבסיסים שונים? מה אם הם לא חזקות מדויקות של אותו מספר?

נוסחאות למעבר לבסיס חדש באות לעזרה. אנו מנסחים אותם בצורה של משפט:

מִשׁפָּט

תן ללוגריתם להירשם a x . ואז לכל מספר c כך ש-c > 0 ו-c ≠ 1, השוויון נכון:

בפרט, אם נשים c = x, נקבל:

מהנוסחה השנייה עולה שאפשר להחליף בין הבסיס לבין הטיעון של הלוגריתם, אבל במקרה זה הביטוי כולו "מתהפך", כלומר. הלוגריתם נמצא במכנה.

נוסחאות אלה נמצאות רק לעתים נדירות בביטויים מספריים רגילים. אפשר להעריך עד כמה הם נוחים רק כאשר פותרים משוואות ואי-שוויון לוגריתמיות.

עם זאת, ישנן משימות שלא ניתן לפתור כלל מלבד מעבר לקרן חדשה. בואו נשקול כמה כאלה:

מצא את הערך של הביטוי: log 5 16 log 2 25.

שימו לב שהארגומנטים של שני הלוגריתמים הם אקספוננטים מדויקים. הבה נוציא את האינדיקטורים: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

כעת נהפוך את הלוגריתם השני:

מכיוון שהמכפלה לא משתנה מתמורה של גורמים, הכפלנו בשלווה ארבע ושתיים, ואז הבנו את הלוגריתמים.

מצא את הערך של הביטוי: log 9 100 lg 3.

הבסיס והטיעון של הלוגריתם הראשון הם חזקות מדויקות. בואו נרשום את זה ונפטר מהאינדיקטורים:

עכשיו בואו נפטר מהלוגריתם העשרוני על ידי מעבר לבסיס חדש:

זהות לוגריתמית בסיסית

לעתים קרובות בתהליך הפתרון נדרש לייצג מספר כלוגריתם לבסיס נתון. במקרה זה, הנוסחאות יעזרו לנו:

במקרה הראשון, המספרנ הופך להיות המעריך של הטיעון. מספרנ יכול להיות כל דבר, כי זה רק הערך של הלוגריתם.

הנוסחה השנייה היא למעשה הגדרה פרפרזה. זה נקרא כך:זהות לוגריתמית בסיסית.

ואכן, מה יקרה אם המספר b יועלה לדרגה כזו שהמספר b בדרגה זו נותן את המספר a? נכון: זה אותו מספר א'. קרא שוב את הפסקה הזו בעיון - אנשים רבים "נתלים" בה.

כמו נוסחאות המרת הבסיס החדשות, הזהות הלוגריתמית הבסיסית היא לפעמים הפתרון האפשרי היחיד.

משימה

מצא את הערך של הביטוי:

הַחְלָטָה

שים לב שיומן 25 64 = יומן 5 8 - פשוט הוציאו את הריבוע מהבסיס והטיעון של הלוגריתם. בהינתן הכללים להכפלת חזקות עם אותו בסיס, אנו מקבלים:

200

אם מישהו לא יודע, זו הייתה משימה אמיתית מהבחינה :)

יחידה לוגריתמית ואפס לוגריתמי

לסיכום, אתן שתי זהויות שקשה לקרוא להן תכונות – אלא, אלו השלכות מהגדרת הלוגריתם. הם נמצאים כל הזמן בבעיות ובאופן מפתיע יוצרים בעיות גם לתלמידים "מתקדמים".

log a a = 1 הוא יחידה לוגריתמית. זכור אחת ולתמיד: הלוגריתם לכל בסיסא מהבסיס הזה עצמו שווה לאחד.

log a 1 = 0 הוא אפס לוגריתמי. בסיס א יכול להיות כל דבר, אבל אם הארגומנט הוא אחד - הלוגריתם הוא אפס! כיא 0 = 1 הוא תוצאה ישירה של ההגדרה.

זה כל הנכסים. הקפד לתרגל ליישם אותם!

היפרמרקט ידע >>מתמטיקה >>מתמטיקה כיתה י' >>

הפונקציה המעריכית, תכונותיה וגרף

שקול את הביטוי 2x ומצא את ערכיו עבור ערכים רציונליים שונים של המשתנה x, למשל, עבור x=2;

באופן כללי, לא משנה איזה ערך רציונלי ניתן למשתנה x, תמיד נוכל לחשב את הערך המספרי המתאים של הביטוי 2x. לפיכך, אפשר לדבר על אקספוננציאלי פונקציות y=2 x מוגדר על קבוצת ה-Q של המספרים הרציונליים:

הבה נבחן כמה מאפיינים של פונקציה זו.

נכס 1.היא פונקציה הולכת וגוברת. אנו מבצעים את ההוכחה בשני שלבים.
במה ראשונה.הבה נוכיח שאם r הוא מספר רציונלי חיובי, אז 2 r >1.
שני מקרים אפשריים: 1) r הוא מספר טבעי, r = n; 2) רגיל בלתי ניתן לצמצום שבריר,

בצד שמאל של אי השוויון האחרון יש לנו , ובצד ימין 1. לפיכך, אי השוויון האחרון יכול להיכתב מחדש כ

כך, בכל מקרה, אי השוויון 2 r > 1 מתקיים, כנדרש.

שלב שני.תנו ל-x 1 ו-x 2 להיות מספרים, ו-x 1 ו-x 2< х2. Составим разность 2 х2 -2 х1 и выполним некоторые ее преобразования:

(סימנו את ההפרש x 2 -x 1 באות r).

מכיוון ש-r הוא מספר רציונלי חיובי, אז לפי מה שהוכח בשלב הראשון, 2 r > 1, כלומר, 2 r -1 >0. המספר 2x" הוא גם חיובי, מה שאומר שהמוצר 2 x-1 (2 Г -1) הוא גם חיובי. לפיכך, הוכחנו ש אי שיוויון 2 Xr -2x "\u003e 0.

אז מהאי-שוויון x 1< х 2 следует, что 2х" <2 x2 , а это и означает, что функция у -2х - возрастающая.

נכס 2.מוגבל מלמטה ולא מוגבל מלמעלה.
הגבול של הפונקציה מלמטה נובע מאי השוויון 2 x > 0, אשר תקף לכל ערכים של x מתחום הפונקציה. יחד עם זאת, לא משנה איזה מספר חיובי M נלקח, תמיד אפשר לבחור באינדיקטור כזה x שיתקיים אי השוויון 2 x > M - מה שמאפיין את חוסר הגבול של הפונקציה מלמעלה. בוא ניתן כמה דוגמאות.

נכס 3.אין לו ערך מינימום ולא מקסימום.

ברור שפונקציה זו אינה בעלת החשיבות הגדולה ביותר, שכן, כפי שראינו זה עתה, היא אינה מוגבלת מלמעלה. אבל הוא מוגבל מלמטה, מדוע אין לו הערך הקטן ביותר?

נניח ש-2r הוא הערך הקטן ביותר של הפונקציה (r הוא מעריך רציונלי כלשהו). קח מספר רציונלי q<г. Тогда в силу возрастания функции у=2 х будем иметь 2 x <2г. А это значит, что 2 r не может служить наименьшим значением функции.

כל זה טוב, אתה אומר, אבל למה אנחנו מחשיבים את הפונקציה y-2 x רק על קבוצת המספרים הרציונליים, למה אנחנו לא מחשיבים אותה, כמו פונקציות מוכרות אחרות, על כל קו המספרים או על מרווח רציף כלשהו של את שורת המספרים? מה עוצר אותנו? בואו נחשוב על המצב.

שורת המספרים מכילה לא רק מספרים רציונליים, אלא גם מספרים אי-רציונליים. עבור הפונקציות שנחקרו בעבר, זה לא הפריע לנו. לדוגמה, מצאנו את הערכים של הפונקציה y \u003d x 2 באותה קלות עבור ערכים רציונליים ואי-רציונליים של x: זה היה מספיק בריבוע את הערך הנתון של x.

אבל עם הפונקציה y \u003d 2 x, המצב מסובך יותר. אם לארגומנט x ניתן ערך רציונלי, אז עקרונית ניתן לחשב את x (חזור לתחילת הפסקה, שם עשינו בדיוק את זה). ואם לארגומנט x ניתן ערך לא רציונלי? איך, למשל, לחשב? אנחנו לא יודעים את זה עדיין.
מתמטיקאים מצאו מוצא; כך הם דיברו.

ידוע ש שקול רצף של מספרים רציונליים - קירובים עשרוניים של מספר לפי חסר:

1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... .

ברור ש-1.732 = 1.7320 ו-1.732050 = 1.73205. כדי להימנע מחזרות כאלה, אנו פוסלים את איברי הרצף המסתיימים בספרה 0.

ואז נקבל רצף הולך וגדל:

1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... .

בהתאם, גם הרצף גדל.

כל האיברים ברצף זה הם מספרים חיוביים פחות מ-22, כלומר. רצף זה מוגבל. לפי משפט ויירשטראס (ראה סעיף 30), אם רצף מתגבר ומתוחם, אז הוא מתכנס. יתרה מכך, מסעיף 30 אנו יודעים שאם רצף מתכנס, אז רק לגבול אחד. גבול יחיד זה סוכם להיחשב כערך של ביטוי מספרי. וזה לא משנה שקשה מאוד למצוא אפילו ערך משוער של הביטוי המספרי 2; חשוב שזה מספר ספציפי (אחרי הכל, לא חששנו לומר שזה, למשל, השורש של משוואה רציונלית, השורש של המשוואה הטריגונומטרית, מבלי לחשוב מה בדיוק המספרים האלה:
אז, גילינו איזו משמעות שמו מתמטיקאים בסמל 2 ^. באופן דומה, ניתן לקבוע מהו ובאופן כללי מהו a, כאשר a הוא מספר אי-רציונלי ו-a > 1.
אבל מה לגבי כאשר 0<а <1? Как вычислить, например, ? Самым естественным способом: считать, что свести вычисления к случаю, когда основание степени больше 1.
עכשיו אנחנו יכולים לדבר לא רק על עצמות עם מעריכים רציונליים שרירותיים, אלא גם על כוחות עם מעריכים ריאליים שרירותיים. הוכח שלמעלות עם כל מעריך ממשי יש את כל המאפיינים הרגילים של מעלות: כשמכפילים מעלות עם אותם בסיסים מוסיפים את המעריכים, כשמחלקים מחסרים אותם, כשמעלים מעלה לחזקה מכפילים אותם וכו'. . אבל הדבר החשוב ביותר הוא שעכשיו אנחנו יכולים לדבר על הפונקציה y-ax המוגדרת בקבוצה של כל המספרים הממשיים.
נחזור לפונקציה y \u003d 2 x, נבנה את הגרף שלה. לשם כך, נערוך טבלה של ערכי פונקציות על ידי 2 x:

נשים לב לנקודות במישור הקואורדינטות (איור 194), הן מתארות קו מסוים, מציירות אותו (איור 195).

מאפייני פונקציה y - 2 x:
1)
2) אינו זוגי ואינו אי זוגי; 248
3) עליות;

5) אין לו את הערכים הגדולים ביותר או הקטנים ביותר;
6) מתמשך;
7)
8) קמור למטה.

הוכחות קפדניות למאפיינים המפורטים של הפונקציה y-2 x ניתנות במהלך מתמטיקה גבוהה יותר. חלק מהמאפיינים הללו שדנו בהם קודם לכן במידה זו או אחרת, חלקם מודגמים בבירור על ידי הגרף הבנוי (ראה איור 195). לדוגמה, היעדר זוגיות או אי זוגיות של פונקציה קשור מבחינה גיאומטרית לחוסר הסימטריה של הגרף, בהתאמה, על ציר ה-y או על המקור.

לכל פונקציה בצורה y=a x, כאשר a >1, יש מאפיינים דומים. על איור. 196 במערכת קואורדינטות אחת בנויים, גרפים של פונקציות y=2 x, y=3 x, y=5 x.

עכשיו בואו נשקול את הפונקציה, בואו נעשה לה טבלת ערכים:

בואו נסמן את הנקודות במישור הקואורדינטות (איור 197), הן מתארות קו מסוים, מציירים אותו (איור 198).

מאפייני פונקציה

1)
2) אינו זוגי ואינו אי זוגי;
3) ירידות;
4) לא מוגבל מלמעלה, מוגבל מלמטה;
5) אין הערכים הגדולים והקטנים ביותר;
6) מתמשך;
7)
8) קמור למטה.
כל פונקציה בצורה y \u003d a x, כאשר O<а <1. На рис. 200 в одной системе координат построены графики функций
שימו לב: גרפי פונקציות הָהֵן. y \u003d 2 x, סימטרי על ציר y (איור 201). זוהי תוצאה של האמירה הכללית (ראה סעיף 13): הגרפים של הפונקציות y = f(x) ו-y = f(-x) הם סימטריים על ציר ה-y. באופן דומה, הגרפים של הפונקציות y \u003d 3 x ו

לסכם את הנאמר, ניתן הגדרה של הפונקציה המעריכית ונדגיש את המאפיינים החשובים ביותר שלה.

הַגדָרָה.פונקציית התצוגה נקראת הפונקציה האקספוננציאלית.
המאפיינים העיקריים של הפונקציה המעריכית y \u003d a x

הגרף של הפונקציה y \u003d a x עבור a> 1 מוצג באיור. 201, ועבור 0<а < 1 - на рис. 202.

העקומה המוצגת באיור. 201 או 202 נקראים המעריך. למעשה, מתמטיקאים בדרך כלל קוראים לפונקציה המעריכית עצמה y = a x. אז המונח "מעריך" משמש בשני מובנים: הן לשם הפונקציה האקספוננציאלית, והן לשם הגרף של הפונקציה המעריכית. בדרך כלל, ברור במשמעות אם אנחנו מדברים על פונקציה אקספוננציאלית או על הגרף שלה.

שימו לב לתכונה הגיאומטרית של הגרף של הפונקציה המעריכית y \u003d ax: ציר ה-x הוא האסימפטוטה האופקית של הגרף. נכון, האמירה הזו בדרך כלל מעודנת באופן הבא.
ציר ה-x הוא האסימפטוטה האופקית של גרף הפונקציה

במילים אחרות

הערה חשובה ראשונה. תלמידי בית ספר מבלבלים לעתים קרובות בין המונחים: פונקציית כוח, פונקציה מעריכית. לְהַשְׁווֹת:

אלו הן דוגמאות לפונקציות כוח;

הן דוגמאות לפונקציות אקספוננציאליות.

באופן כללי, y \u003d x r, כאשר r הוא מספר מסוים, היא פונקציית חזקה (הארגומנט x כלול בבסיס התואר);
y \u003d a", כאשר a הוא מספר מסוים (חיובי ושונה מ-1), היא פונקציה מעריכית (הארגומנט x כלול במעריך).

פונקציה "אקזוטית" תוקפת כמו y = x" אינה נחשבת לא מעריכית ולא לחוק החזקה (לפעמים היא נקראת פונקציית חזקה מעריכית).

הערה חשובה שניה. בדרך כלל, לא מחשיבים פונקציה מעריכית עם בסיס a = 1 או עם בסיס a המקיים את אי השוויון a<0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0and a העובדה היא שאם \u003d 1, אז עבור כל ערך x השוויון Ix \u003d 1 נכון. לפיכך, הפונקציה המעריכית y \u003d a "for a \u003d 1" מידרדרת "לפונקציה קבועה y \ u003d 1 - זה לא מעניין. אם \u003d 0, אז 0x \u003d 0 עבור כל ערך חיובי של x, כלומר נקבל את הפונקציה y \u003d 0 מוגדרת עבור x\u003e 0 - זה גם לא מעניין.<0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках.

לפני שנעבור לפתרון דוגמאות, נציין שהפונקציה האקספוננציאלית שונה משמעותית מכל הפונקציות שלמדת עד כה. כדי ללמוד ביסודיות אובייקט חדש, אתה צריך לשקול אותו מזוויות שונות, במצבים שונים, כך שיהיו דוגמאות רבות.
דוגמה 1

הַחְלָטָה, א) לאחר ששרטטנו את הגרפים של הפונקציות y \u003d 2 x ו- y \u003d 1 במערכת קואורדינטות אחת, אנו מבחינים (איור 203) שיש להם נקודה משותפת אחת (0; 1). אז למשוואה 2x = 1 יש שורש בודד x = 0.

אז מהמשוואה 2x = 2° קיבלנו x = 0.

ב) לאחר שבנו את הגרפים של הפונקציות y \u003d 2 x ו- y \u003d 4 במערכת קואורדינטות אחת, אנו מבחינים (איור 203) שיש להם נקודה משותפת אחת (2; 4). אז למשוואה 2x = 4 יש שורש יחיד x = 2.

אז מהמשוואה 2 x \u003d 2 2 קיבלנו x \u003d 2.

ג) ו-ד) בהתבסס על אותם שיקולים, אנו מסיקים כי למשוואה 2 x \u003d 8 יש שורש בודד, וכדי למצוא אותו, לא ניתן לבנות גרפים של הפונקציות המתאימות;

ברור ש-x=3, שכן 2 3 =8. באופן דומה, אנו מוצאים את השורש היחיד של המשוואה

אז מהמשוואה 2x = 2 3 קיבלנו x = 3, ומהמשוואה 2 x = 2 x קיבלנו x = -4.
ה) הגרף של הפונקציה y \u003d 2 x ממוקם מעל הגרף של הפונקציה y \u003d 1 עבור x\u003e 0 - זה נקרא היטב באיור. 203. לפיכך, הפתרון לאי השוויון 2x > 1 הוא המרווח
ו) הגרף של הפונקציה y \u003d 2 x ממוקם מתחת לגרף של הפונקציה y \u003d 4 ב-x<2 - это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток
בטח שמתם לב שהבסיס לכל המסקנות שהתקבלו בעת פתרון דוגמה 1 היה תכונת המונוטוניות (עלייה) של הפונקציה y \u003d 2 x. נימוק דומה מאפשר לנו לאמת את תקפותם של שני המשפטים הבאים.

הַחְלָטָה.אתה יכול לפעול כך: לבנות גרף של הפונקציה y-3 x, ואז למתוח אותו מציר ה-x עם גורם של 3, ולאחר מכן להעלות את הגרף שנוצר ב-2 יחידות קנה מידה. אבל זה יותר נוח להשתמש בעובדה ש-3- 3* \u003d 3 * + 1, ולכן, לצייר את הפונקציה y \u003d 3 x * 1 + 2.

נעבור, כפי שעשינו שוב ושוב במקרים כאלה, למערכת קואורדינטות עזר עם המוצא בנקודה (-1; 2) - קווים מנוקדים x = - 1 ו- 1x = 2 באיור. 207. בואו "נצרף" את הפונקציה y=3* למערכת קואורדינטות חדשה. לשם כך, אנו בוחרים נקודות בקרה עבור הפונקציה , אבל נבנה אותם לא בישן, אלא במערכת הקואורדינטות החדשה (נקודות אלו מסומנות באיור 207). לאחר מכן נבנה מעריך לפי נקודות - זה יהיה הגרף הנדרש (ראה איור 207).
כדי למצוא את הערכים הגדולים והקטנים ביותר של פונקציה נתונה בקטע [-2, 2], אנו משתמשים בעובדה שהפונקציה הנתונה הולכת וגדלה, ולכן היא לוקחת את הערכים הקטן והגדול ביותר שלה, בהתאמה, בצד שמאל וב הקצוות הימניים של הקטע.
כך:

דוגמה 4פתור את המשוואה ואי השוויון:

הַחְלָטָה, א) בואו נבנה גרפים של פונקציות y=5* ו-y=6-x במערכת קואורדינטות אחת (איור 208). הם מצטלבים בנקודה אחת; אם לשפוט לפי הציור, זו הנקודה (1; 5). הבדיקה מראה שלמעשה הנקודה (1; 5) עומדת הן במשוואה y = 5* והן את המשוואה y=6x. האבססיס של נקודה זו משמשת כשורש היחיד של המשוואה הנתונה.

לכן, למשוואה 5 x = 6-x יש שורש בודד x = 1.

ב) ו-ג) המעריך y-5x נמצא מעל הישר y=6-x, אם x>1, - זה נראה בבירור באיור. 208. מכאן שניתן לכתוב את הפתרון של אי השוויון 5*>6-x כך: x>1. והפתרון של אי השוויון פי 5<6 - х можно записать так: х < 1.
תשובה: א) x = 1; ב)x>1; ג) x<1.

דוגמה 5נתונה פונקציה תוכיח את זה
הַחְלָטָה.לפי תנאי יש לנו.

פונקציות אקספוננציאליות ולוגריתמיות VIII

§ 179 מאפיינים בסיסיים של הפונקציה המעריכית

בחלק זה נלמד את המאפיינים העיקריים של הפונקציה האקספוננציאלית

y = א איקס (1)

תזכור את זה מתחת א בנוסחה (1) אנו מתכוונים לכל מספר חיובי קבוע שאינו 1.

נכס 1. התחום של הפונקציה המעריכית הוא קבוצת כל המספרים הממשיים.

אכן, לחיוב א ביטוי א איקס מוגדר עבור כל מספר ממשי איקס .

נכס 2. הפונקציה המעריכית לוקחת רק ערכים חיוביים.

אכן, אם איקס > 0, אם כן, כפי שהוכח בסעיף 176,

א איקס > 0.

אם איקס <. 0, то

א איקס =

איפה - איקס כבר גדול מאפס. בגלל זה א - איקס > 0. אבל אז

א איקס = > 0.

לבסוף, ב איקס = 0

א איקס = 1.

למאפיין השני של הפונקציה האקספוננציאלית יש פרשנות גרפית פשוטה. זה טמון בעובדה שהגרף של פונקציה זו (ראה איור 246 ו-247) ממוקם כולו מעל ציר ה-x.

נכס 3. אם א >1, ואז ב איקס > 0 א איקס > 1, וב איקס < 0 א איקס < 1. אם א < 1, тאה, להיפך, איקס > 0 א איקס < 1, וב איקס < 0 א איקס > 1.

תכונה זו של הפונקציה האקספוננציאלית מאפשרת גם פרשנות גיאומטרית פשוטה. בְּ א > 1 (איור 246) עקומות y = א איקס ממוקם מעל הקו בְּ- = 1 ב איקס > 0 ומתחת לקו הישר בְּ- = 1 ב איקס < 0.

אם א < 1 (рис. 247), то, наоборот, кривые y = א איקס ממוקם מתחת לקו בְּ- = 1 ב איקס > 0 ומעל לקו הישר הזה ב איקס < 0.

תן לנו לתת הוכחה קפדנית של הנכס השלישי. תן להיות א > 1 ו איקס הוא מספר חיובי שרירותי. בואו נראה את זה

א איקס > 1.

אם מספר איקס רציונלי ( איקס = M / נ ) , לאחר מכן א איקס = א M / נ = נ √א M .

בגלל ה א > 1, אז א M > 1, אבל השורש של מספר גדול מאחד הוא כמובן גם גדול מ-1.

אם איקס לא רציונלי, אז יש מספרים רציונליים חיוביים איקס" ו איקס" , המשמשים כקירוב עשרוני של המספר איקס :

איקס"< х < х" .

אבל אז, בהגדרה של תואר עם מעריך לא רציונלי

א איקס" < א איקס < א איקס"" .

כפי שמוצג לעיל, המספר א איקס" יותר מאחד. לכן, המספר א איקס , יותר מ א איקס" , חייב להיות גם גדול מ-1,

אז, הראינו את זה א >1 וחיובי שרירותי איקס

א איקס > 1.

אם המספר איקס היה שלילי, אז היינו צריכים

א איקס =

איפה המספר איקס יהיה חיובי. בגלל זה א - איקס > 1. לכן,

א איקס = < 1.

לפיכך, ב א > 1 ושלילי שרירותי איקס

א איקס < 1.

מקרה כאשר 0< א < 1, легко сводится к уже рассмотренному случаю. Учащимся предлагается убедиться в этом самостоятельно.

נכס 4. אם x = 0, ואז בלי קשר לא א איקס =1.

הדבר נובע מהגדרת תואר אפס; חזקת האפס של כל מספר שאינו אפס שווה ל-1. מבחינה גרפית, תכונה זו מתבטאת בעובדה שעבור כל א עֲקוּמָה בְּ- = א איקס (ראה איור 246 ו-247) חוצה את הציר בְּ- בנקודה עם סמין 1.

נכס 5. בְּ א >1 פונקציה מעריכית = א איקס עולה באופן מונוטוני, ובמשך א < 1 - יורד באופן מונוטוני.

תכונה זו מאפשרת גם פרשנות גיאומטרית פשוטה.

בְּ א > 1 (איור 246) עקומה בְּ- = א איקס עם צמיחה איקס עולה יותר ויותר, ו א < 1 (рис. 247) - опускается все ниже и ниже.

תן לנו לתת הוכחה קפדנית של הנכס החמישי.

תן להיות א > 1 ו איקס 2 > איקס אחד . בואו נראה את זה

א איקס 2 > א איקס 1

בגלל ה איקס 2 > איקס 1., אז איקס 2 = איקס 1 + ד , איפה ד הוא מספר חיובי כלשהו. בגלל זה

א איקס 2 - א איקס 1 = א איקס 1 + ד - א איקס 1 = א איקס 1 (א ד - 1)

לפי התכונה ה-2 של הפונקציה האקספוננציאלית א איקס 1 > 0. מאז ד > 0, ואז לפי התכונה ה-3 של הפונקציה האקספוננציאלית א ד > 1. שני הגורמים במוצר א איקס 1 (א ד - 1) הם חיוביים, ולכן המוצר הזה עצמו חיובי. אומר, א איקס 2 - א איקס 1 > 0, או א איקס 2 > א איקס 1, שהיה צריך להוכיח.

אז, ב א > פונקציה אחת בְּ- = א איקס עולה באופן מונוטוני. באופן דומה, הוכח כי א < 1 функция בְּ- = א איקס יורד באופן מונוטוני.

תוֹצָאָה. אם שתי חזקות של אותו מספר חיובי מלבד 1 שווים, אז גם המעריכים שלהן שווים.

במילים אחרות, אם

א ב = א ג (א > 0 ו א =/= 1),

b = c .

אכן, אם המספרים ב ו עם לא היו שווים, אז בגלל המונוטוניות של הפונקציה בְּ- = א איקס רובם יתאימו ל א >1 גדול יותר, וב- א < 1 меньшее значение этой функции. Таким образом, было бы или א ב > א ג , או א ב < א ג . שני אלה סותרים את התנאי א ב = א ג . נותר להכיר בכך b = c .

נכס 6. אם > 1, ואז עם עלייה בלתי מוגבלת בטיעון איקס (איקס -> ∞ ) ערכי פונקציות בְּ- = א איקס גם לגדול ללא הגבלת זמן (בְּ- -> ∞ ). עם ירידה בלתי מוגבלת בטיעון איקס (איקס -> -∞ ) הערכים של פונקציה זו נוטים לאפס, בעוד שהם נשארים חיוביים (בְּ-->0; בְּ- > 0).

תוך התחשבות במונוטוניות שהוכחה לעיל של הפונקציה בְּ- = א איקס , אנו יכולים לומר שבמקרה הנדון, הפונקציה בְּ- = א איקס גדל באופן מונוטוני מ-0 ל ∞ .

אם 0 <א < 1, אז עם עלייה בלתי מוגבלת בארגומנט x (x -> ∞), ערכי הפונקציה y \u003d a x שואפים לאפס, בעוד שהם נשארים חיוביים (בְּ-->0; בְּ- > 0). עם ירידה בלתי מוגבלת בארגומנט x (איקס -> -∞ ) הערכים של פונקציה זו גדלים ללא הגבלת זמן (בְּ- -> ∞ ).

בשל המונוטוניות של הפונקציה y = גרזן אנו יכולים לומר שבמקרה זה הפונקציה בְּ- = א איקס יורד מונוטוני מ ∞ ל-0.

התכונה ה-6 של הפונקציה המעריכית משתקפת בבירור באיורים 246 ו-247. לא נוכיח זאת בקפדנות.

אנחנו צריכים רק לקבוע את הטווח של הפונקציה האקספוננציאלית y = גרזן (א > 0, א =/= 1).

למעלה הוכחנו שהפונקציה y = גרזן לוקח רק ערכים חיוביים ואחד עולה באופן מונוטוני מ-0 ל ∞ (בְּ א > 1), או יורד מונוטוני מ ∞ ל-0 (ב-0< א <. 1). Однако остался невыясненным следующий вопрос: не претерпевает ли функция y = גרזן כאשר אתה משנה קפיצות כלשהן? האם זה דורש ערכים חיוביים? שאלה זו נענית בחיוב. אם א > 0 ו א =/= 1, ואז יהיה המספר החיובי אשר יהיה בְּ- יש למצוא 0 איקס 0, כזה

א איקס 0 = בְּ- 0 .

(בשל המונוטוניות של הפונקציה y = גרזן ערך שצוין איקס 0 יהיה היחיד, כמובן.)

ההוכחה לעובדה זו היא מעבר למסגרת התוכנית שלנו. הפרשנות הגיאומטרית שלו היא שלכל ערך חיובי בְּ- גרף פונקציות 0 y = גרזן חייב להצטלב עם הקו בְּ- = בְּ- 0 ויותר מכך, רק בנקודה אחת (איור 248).

מכאן נוכל להסיק את המסקנה הבאה, אותה אנו מנסחים בצורת מאפיין 7.

נכס 7. אזור השינוי של הפונקציה המעריכית y \u003d a x (א > 0, א =/= 1)הוא קבוצת כל המספרים החיוביים.

תרגילים

1368. מצא את התחומים של הפונקציות הבאות:

1369. איזה מהמספרים הנתונים גדול מ-1 ואיזה קטן מ-1:

1370. על בסיס איזו תכונה של הפונקציה המעריכית ניתן לטעון זאת

א) (5/7) 2.6 > (5/7) 2.5; ב) (4/3) 1.3 > (4/3) 1.2

1371. איזה מספר גדול יותר:

א) π - √3 או (1 / π ) - √3; ג) (2/3) 1 + √6 או (2/3) √2 + √5 ;

ב) ( π / 4) 1 + √3 או ( π / 4) 2; ד) (√3 ) √2 - √5 או (√3) √3 - 2 ?

1372. האם אי השוויון שווה ערך:

1373. מה ניתן לומר על מספרים איקס ו בְּ- , אם a x = ו-y , איפה א האם מספר חיובי נתון?

1374. 1) האם זה אפשרי בין כל הערכים של פונקציה בְּ- = 2איקס שִׂיא:

2) האם זה אפשרי בין כל ערכי הפונקציה בְּ- = 2 | x| שִׂיא:

א) הערך הגדול ביותר; ב) הערך הקטן ביותר?